TLA+ 入門

TLA+は、MicrosoftやAmazonがミドルウェアの設計に利用しているステートマシンの記述言語です。実際、Azure Cosmos DBやAmazon DynamoDB, S3, EBSはTLA+を使って設計、検証を行っていると公式に発表されています。

• AmazonはどのようにTLA+を利用しているか
• Azure Cosmos DBの設計・開発におけるTLA+の貢献

IDEのダウンロードとインストール

TLA+はTLA ToolboxというIDEが用意されており、シンタックスチェックや、作成したステートマシンの検証を行うことが可能です。TLA Toolboxは下記のGitHubのリンクからダウンロードが可能で、利用するにはJava 1.8以上が必要です。

• ダウンロード先

ステートマシンの記述

TLA+は、JavaやPythonなどでのプログラミングと以下の点で異なります。

• 数学的な表記方法
• どう実装するかではなく、どう動くかを記述

それでは簡単なPythonコードとTLA+コードを比較してみましょう。

以下は、1か2の乱数を取得し、それに1を加えるPythonプログラムです。乱数の取得方法は、現在のタイムスタンプを2で割ることによって実装しています。

import time

def getRandNum():
    return (int(time.time()) % 2) + 1

def addOne(i):
    return i + 1

i = getRandNum()
i = addOne(i)

# debug
print(i)

TLA+では、初期状態Initと次の状態Nextを使って表現します。以下がTLA+での記述例です。

EXTENDS Integers

VARIABLES pc, i

Init == i = 0 /\ pc = "start"

Rand1 == /\ pc = "start"
         /\ i' = 1
         /\ pc' = "middle"

Rand2 == /\ pc = "start"
         /\ i' = 2
         /\ pc' = "middle"

Add1 == /\ pc = "middle"
        /\ i' = i + 1
        /\ pc' = "done"

Next == Rand1 \/ Rand2 \/ Add1

TLA+では数学的な記法を用いており、JavaやPythonでは見られない記法が用いられています。おおざっぱに各記号は下記を意味しています。

• == … “定義する”という意味。Init == i = 0 /\ pc = “start”は、i = 0 /\ pc = “start”にInitという名前をつけている。
• = … “等しい”という意味。i = 0は変数iがゼロに等しいかを調べる。
• /\ … “かつ”という意味。i = 0 /\ pc = “start”は変数iがゼロかつ、変数pcがstartに等しいことを表す。
• \/ … “または”という意味。Rand1 \/ Rand2 \/ Add1はRand1か、Rand2か、Add1という意味になる。
• X’ … “Xの次の状態”という意味。i’ = i + 1は変数iを1追加して更新することを表す。

特に「=」の使い方がプログラミング言語での使い方と逆なので注意が必要です。

TLA+では、どのように実装するかは議論しないので、Pythonコードに見られたタイムスタンプを使って乱数を生成するところは記述しません。

TLA+では、前提条件preconditionと事後条件postconditionを使って記述します。例えば、Rand1では、前提条件pc=”start”が満たされれば、変数pcを”middle”、変数iを1に変更します。初期状態Initで、変数pcは”start”が代入されているので、初期状態の後、Rand1を実行することができます。また、Rand2も同じ前提条件pc=”start”ですが、Add1は前提条件pc=”middle”なので、初期状態の後Rand1かRand2は起こりますが、Add1は起こりません。これはPythonコードの実行順序（i=getRandNumのあと、i=addOne(i)）に一致しています。初期状態から、Rand1とRand2の両方が実行可能というのは、PythonコードでgetRandNumが1か2を返すのか決定的でないことと同じです。

ステートマシンの実行

実際に、上記のTLA+をTLA Toolboxで実行してみましょう。インストールしたTLA Toolboxを起動し、File -> Open Spec -> Add New Spec…をクリックします。適当なディレクトリを指定し、Finishをクリックします。ここではSampleという名前にしました。

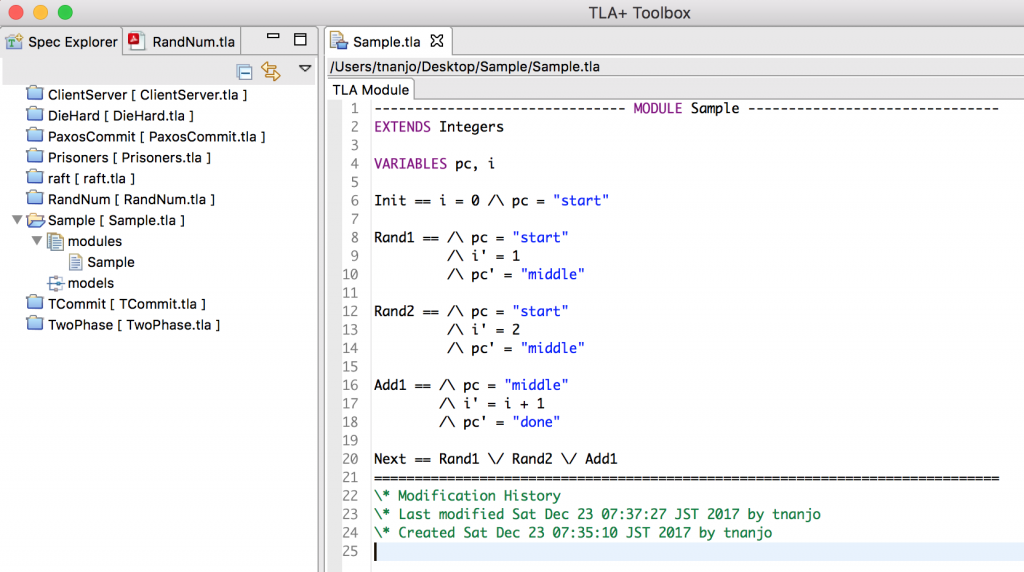
上記のコードを「—-MODULE Sample—-」「======」の間にコピペして、保存します。保存すると自動で、更新日時がコメントとして挿入されます。

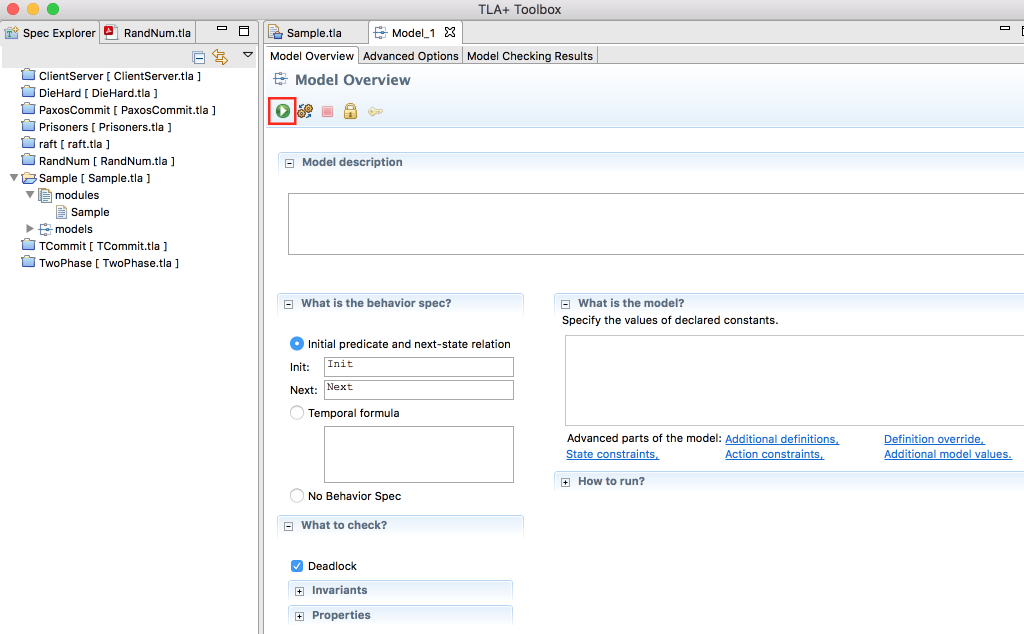
では、TLC Model Checker->New Modelをクリックして、新しいモデルをつくります。ここでは、名前を「Model_1」として作成しました。作成できたら、赤枠にある実行ボタンを押してみます。

実行が完了すると、「Deadlock reached」というエラーがでると思います。今回は、乱数を生成し、1を追加した後のステップは用意されていないモデルなので、デッドロックとなります。Model Overviewタブをクリックして、Deadlockの検証を外します。

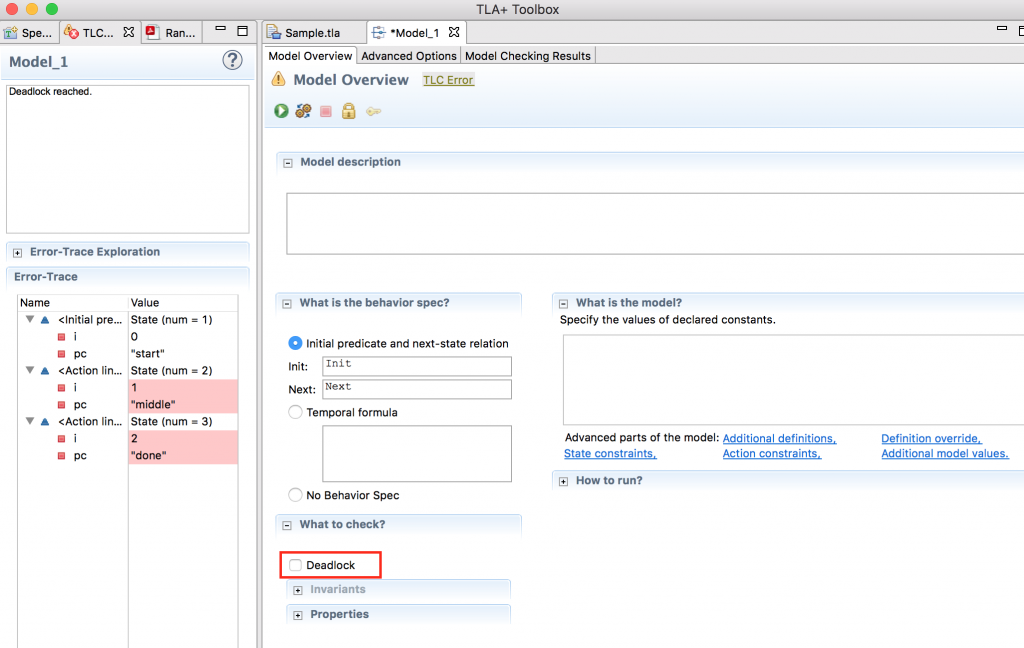
ステートマシンの検証

書いたプログラムをテストコードでテストするように、TLA+で作ったステートマシンもテスト（検証）することが可能で、この試験により設計上のバグを見つけることができます。ステートマシンの検証では、全てのステートで成り立つ不変量Invariantと、ステートマシンの性質を定義したPropertyの2種類を調べられます。

Invariant

今回の例では、乱数1、2に対して1を加えるので、変数iは常に0から3までの数値です。これをInvariantを使って検証します。

Next == Rand1 \/ Rand2 \/ Add1 の次の行に、下記を追加します。

-------
NumberLimit == i \in {0,1,2,3}

i \in {0,1,2,3}は、変数iが集合{0,1,2,3}の要素であることを示しています。モデルのタブをクリックして、上記のInvariantを追加します。Invariants欄のAddをクリックして、NumberLimitと入力してFinishをクリックします。

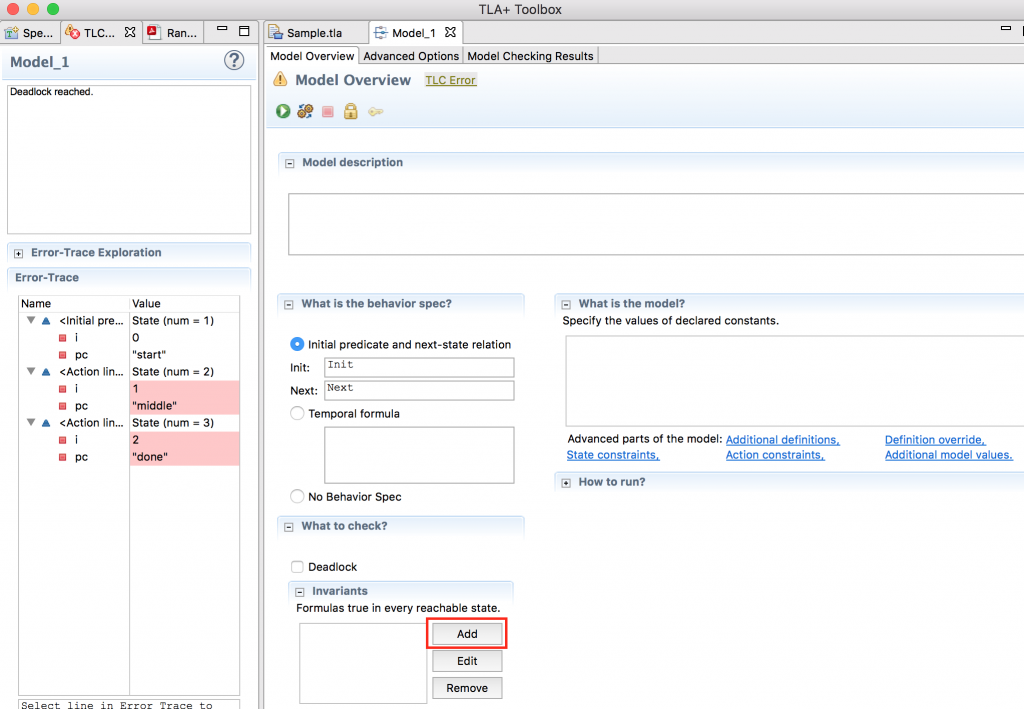
NumberLimitを追加できたら、緑色の再生ボタンを押して、再びモデルを実行します。Error Detectedの欄が「No errors」になることがわかると思います。これは、変数iが全てのステートで0から3までの数値であることを示しています。それでは、先程のコードを変更して、エラーを起こしてみましょう。NumberLimitを下記のように変更して、再びモデルタブから再生ボタンを押してみます。

-------
NumberLimit == i \in {0,1,2}

さて今回は、下記のようにエラーがでると思います。左のパネルではトレースというエラーにいたるまでのステートの変化が表示されています。今回は、乱数が2のとき、1を加えた結果が3になることを表しています。このようにして、全てのステートで成立すべき性質をTLA Toolboxに調べさせることができます。

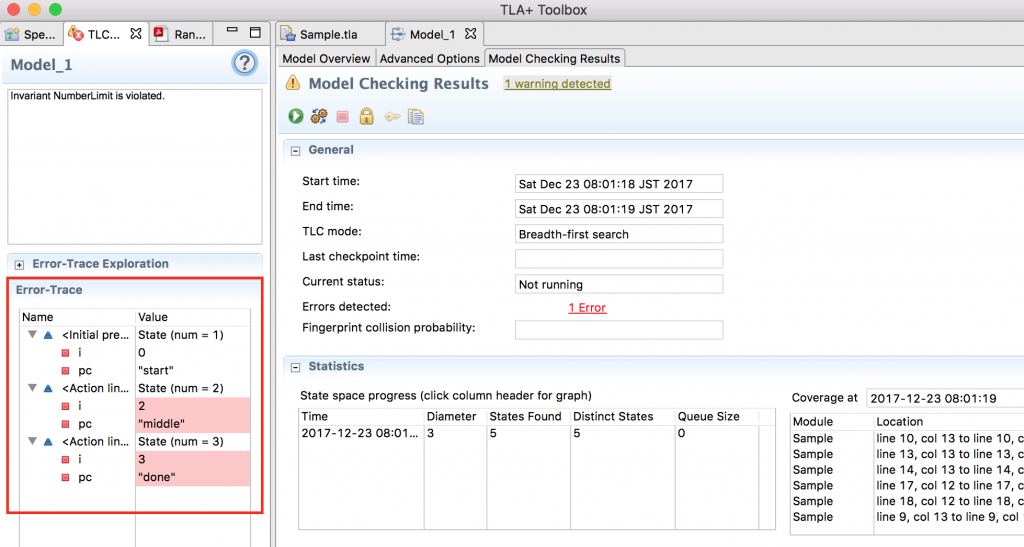
Property

さて、Invariantは全てのステートで成り立つ性質の話でしたが、もうすこし複雑な性質を検証したい場合、Propertyを使います。エディタに戻り、NumberLimitの下に以下のコードを追加します。

NumberLimit == i \in {0,1,2,3} /* {0,1,2,3}に修正する */
Done == [](pc = "done" => i>1)

[](pc = "done" => i>1) は、Temporal Logicを使った記述方法で、変数pcがdoneのとき（すなわち変数iに1を加え終わったとき）、変数iは1より大きいということを表しています。モデルのタブをクリックして、上記のPropertyを追加します。Properties欄のAddをクリックして、Doneと入力してFinishをクリックします。

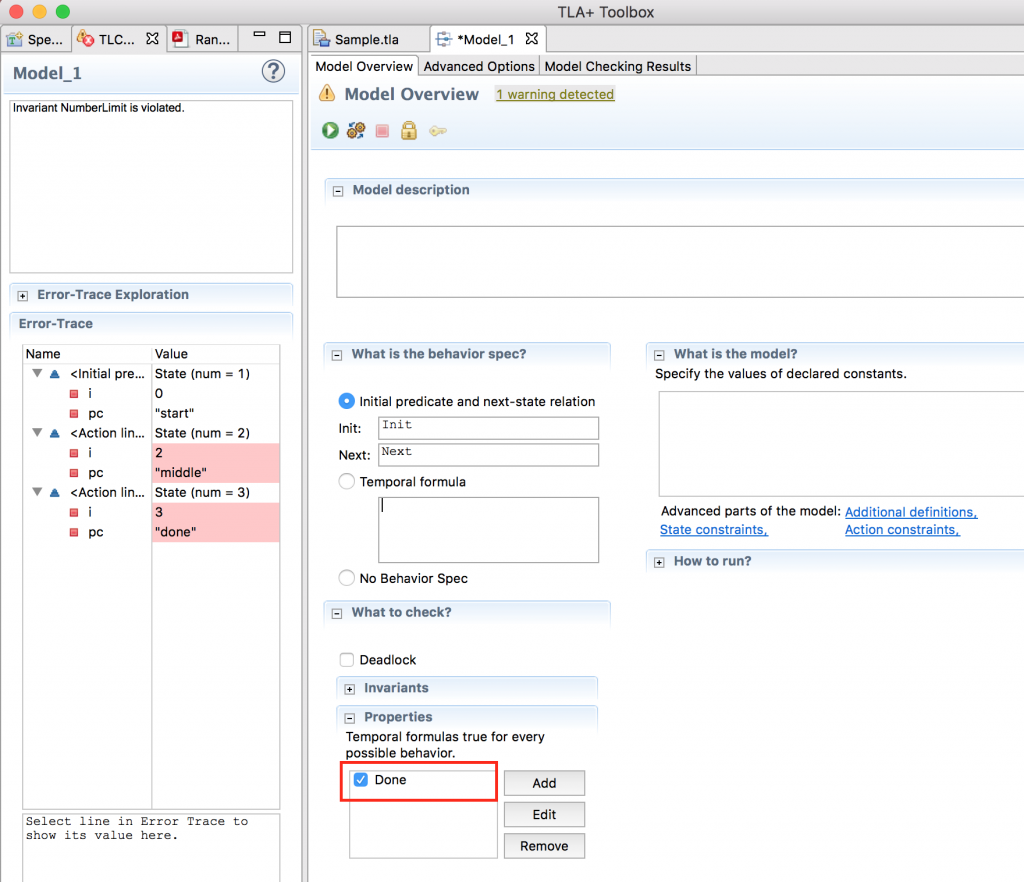
緑色の再生ボタンを押して、Error Detectedの欄が「No errors」になれば、「変数iに1を加え終わったとき、変数iは必ず1よりも大きい」という性質が満たされていることがわかります。

まとめ

今回はTLA+を紹介しました。TLA+は設計用の言語なので、その実装方法については触れず、前提条件が満たされた場合に何が起こるのか、事後条件を記述していきます。TLA+で記述することで、実装前から試験が可能になり、仕様上のバグがないかどうか調べることがことできます。さらにTLA+を知りたいという方は、下記のビデオコースがおすすめです。

• The TLA+ Video Course